„Für uns ist die FEM außerordentlich wichtig. Ohne sie wäre ein extremer Leichtbau, wie wir ihn im Kranbau einsetzen, nicht denkbar. Wir könnten unseren Kunden keine Krane bieten, die einerseits starke Traglasten haben und andererseits wirtschaftlich auf der Straße bewegt werden können.

Unser tägliches Brot in der Statik ist die Frage, wie stark das Material durch äußere Kräfte beansprucht wird. Die Beanspruchungen von geometrisch einfachen Formen wie Stab oder Quader können nach bekannten physikalischen Formeln berechnet werden. Aber wie berechnet man komplexere Formen, für die es keine Formeln gibt? Genau hier kommt die Finite-Elemente-Methode ins Spiel.

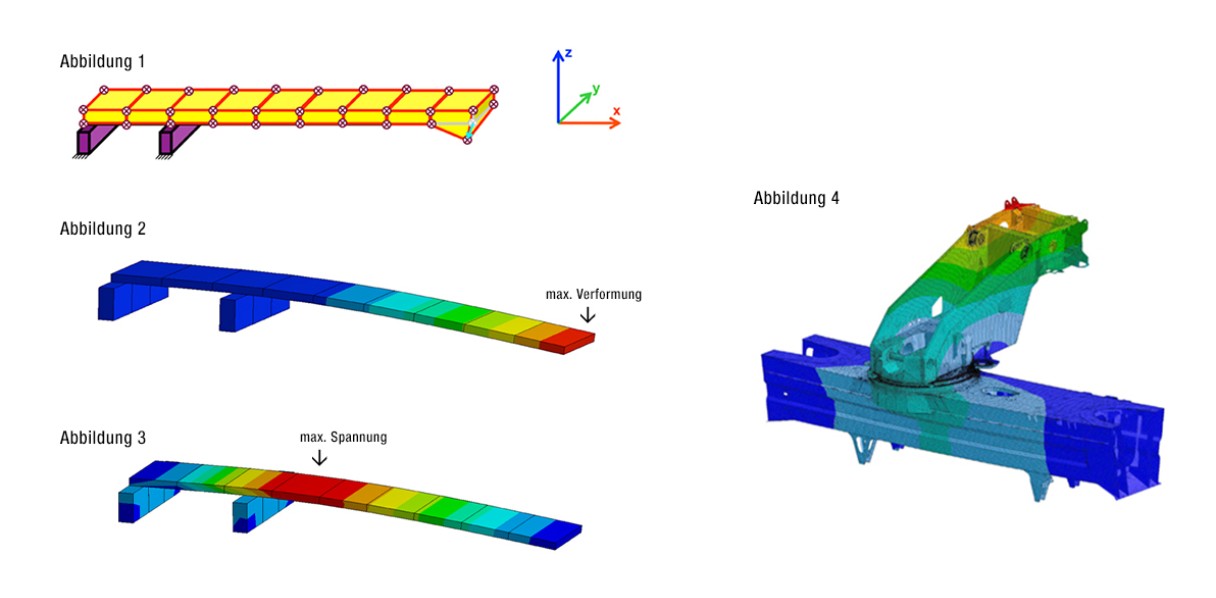
Machen wir ein ganz einfaches Beispiel (siehe Abbildung 1): Ein langer schmaler Körper wird in neun finite Elemente zerlegt. Dabei entstehen 40 Knotenpunkte, die die Elemente verbinden. Jeder Knotenpunkt kann sich unter Belastung in die drei Raumrichtungen x, y und z verformen. Insgesamt ergeben sich also 40 x 3 = 120 unbekannte Verformungen. Zur Lösung benötigt man 120 lineare Gleichungen. Abbildung 2 zeigt die Verformungen, die sich nach dem Lösen des Gleichungssystems ergeben, Abbildung 3 die aus den Verformungen abgeleiteten Spannungen im Körper. Für beide Darstellungen gilt: je roter, desto größer. Bei der Berechnung unserer Krane haben wir es natürlich mit wesentlich mehr kleinen Elementen und daher mit Millionen von Gleichungen zu tun. Je mehr Elemente, desto genauer ist das Ergebnis. Dennoch ist FEM immer ein Näherungsverfahren. Abbildung 4 zeigt die FEM-Auswertung bezüglich der Verformung einer Drehbühne auf einem Fahrzeugrahmen.

Die FEM bietet uns die Möglichkeit, viele verschiedene Konstruktionsideen zu bewerten, ohne sie physisch bauen zu müssen. Dadurch können wir schneller neue Lösungen entwickeln und auf den Markt bringen.“

Dieser Artikel erschien im UpLoad Magazin 02 | 2019.